[OVERLINE]المصفوفات[/OVERLINE]
عمل الطالب:.............
الصف:.............
باشراف الاستاذ:........
الفهرس:1-المصفوفات عامة
2-جمع المصفوفات
3-ضرب المصفوفات
4-معكوس المصفوفات
5-النهاية
المصفوفات
مكن تعريف المصفوفة عامة على أنها دالة رياضية خطية تحول مجموعة بداية أي انطلاق (مجال) إلى مجموعة وصول أو نهاية (مدى). مجموعة الانطلاق و الوصول يمكن أن تكون متكونة من أعداد صحيحة أو عقدية أو أشعة من الأعداد كما يمكن أن تكون هاتان المجموعتان متكونة بدورها من دالات رياضية أو أشعة دالات رياضية. و يمكن أن نرمز للمصفوفة بمعقفين يكتب بينهما عناصر المصفوفة كما هو مبين أسفله:

حيث aij يمكن أن تكون أعدادا صحيحة أو مركبة كما يمكن أن تكون دالات رياضية. ==
ن مصفوفة من الشكل  ، هي عبارة عن تابع:
، هي عبارة عن تابع:  إن
إن  هو الجداء الديكارتي لكل من
هو الجداء الديكارتي لكل من و
و 
الجمع
لكى يتسنى جمع مصفوفتين فلابد ان يكونا من نفس الحيز. و يعرف حاصل جمع مصفوفتين بأنه المصفوفة الناتجة من جمع العناصر المتناظرة في المصفوفتين. فعلى سبيل المثال إذا كان
ِ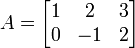 ,
, فإن
فإن 
و بصفة عامة إذا كان
Amxn = aij,Bmxn = bij
فإن A + B هي مصفوفة جديدة Cmxn = cij حيث
cij = aij + bij
الضرب
ضرب مصفوفة وحيدة العنصر مع مصفوفة متعددة العناصر
نضرب العنصر الوحيد مع كل عنصر من عناصر المصفوفة، وتكون النتيجة، مصفوفة جديدة، تحوي العدد نفسه من العناصر. 
[عدل] ضرب مصفوفة في مصفوفة
يجب في البداية أن نعلم أن ضرب المصفوفات غير تبديلي.
من أجل إيجاد ناتج ضرب مصفوفتين (وهو مصفوفة)، يجب أن يتحقق الشرط التالي:
عدد الأعمدة في المصفوفة الأولى = عدد الأسطر في مصفوفة الثانية
بفرض A مصفوفة من الشكل a x b، وB مصفوفة من الشكل c x d، فمن أجل إيجاد A * B، يجب أن يكون b=c.
سنبدأ في البداية بضرب مصفوفة وحيدة السطر مع مصفوفة وحيدة العمود، فبفرض A وB مصفوفتان، حيث:


فيكون: 
ونلاحظ أن المصفوفة الناتجة هي مصفوفة وحيدة العنصر، وبالتالي، فإن ضرب مصفوفة وحيدة السطر مع مصفوفة وحيدة العمود ينتج مصفوفة وحيدة العنصر.
أما عند ضرب مصفوفتين متعددتي العناصر (وبفرض تحقق شروط الضرب)، فعندئذ، نقوم بتقسيم المصفوفة الأولى إلى سطور، والثانية إلى أعمدة، ونقوم بضرب الصف الأول بالعمود الأول (والنتيجة هي العنصر a_11 من النتيجة)، ثم نقوم بضرب الصف الأول مرة أخرى بالعمود الثاني (والنتيجة هي العنصر a_12 من النتيجة، وهكذا.
[عدل] أمثلة على الضرب
مثال توضيحي بالرموز:
بفرض: 
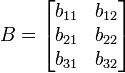
فيكون:

مثال بالأرقام:


معكوس المصفوفة يقصد به المعكوس الضربى للمصفوفة بحيث يكون حاصل ضرب المصفوفة فى معكوسها يساوى مصفوفة الوحدة
ايجاد معكوس المصفوفة
يمكن ايجاد معكوس المصفوفة من القانون التالى: A − 1 = (1 / | A | )adjA |A| يقصد بها محددة المصفوفة و adj A هى المصفوفة المرتبطة
المصفوفة الشاذة
هى المصفوفة التى ليس لها معكوس ويمكن تحديد ما اذا كانت المصفوفة شاذة او لا اذا كانت 0=|a|فهى مصفوفة شاذة
لحساب معكوس المصفوفة
حساب محددة المصفوفة والتاكد انه لا يساوى صفر
حساب المصفوفة المرتبطة
حساب المعكوس
خواص معكوس المصفوفة
معكوس خاصل ضرب مصفوفتين غير شاذتين يساوى حاصل ضرب معكوس كل من المصفوفتين
معكوس مدور المصفوفة يساوى مدور نعكوس المصفوفة
اتمنى يعجبكم
مع تحياتي:ابن سوريا123
اعطوني رأيكم.png)
، هي عبارة عن تابع:
إن
هو الجداء الديكارتي لكل من
و
,
فإن
